Fractales : outil de prévision des marchés financiers ?

Par Gilles Abramson – Directeur associé chez Arborescence Capital
Pour comprendre l’intérêt des fractales appliquées aux marchés financiers, il est nécessaire d’évoquer d’abord l’origine de ce terme, notion qui sera complétée par d’autres paramètres permettant de mieux appréhender la vraie nature des marchés et l’apport de ces éléments dans la ,gestion de portefeuille.
Le terme Fractale a été inventé par Benoit Mandelbrot, mathématicien franco-américain, qui s’intéressa particulièrement aux phénomènes irréguliers de toute sorte tant au niveau mathématique, physique, biologique ou économique. En effet la géométrie fractale s’applique mieux à notre environnement, au sens le plus général, que la géométrie des formes lisses comme par exemple celle d’Euclide. Pour prendre deux exemples simples : les montagnes ne sont pas des cônes, de même les marchés financiers ne peuvent être résumés à des oscillations périodiques ni à des droites montantes ou descendantes…
Au sens le plus général, on parle de fractale pour un objet qui a des formes irrégulières ou fragmentées. Un exemple des plus connus concerne la structure d’un flocon de neige, mais les fractales peuvent aussi s’appliquer, par exemple, à un chou-fleur, aux montagnes, aux nuages, aux arbres, aux vaisseaux sanguins ou bien encore aux côtes de la Bretagne. Mais, outre son caractère irrégulier – Mandelbrot parlait de rugosité – une fractale est caractérisée par l’invariance d’échelle.
Dit autrement, c’est le fait de retrouver les mêmes structures ou motifs quel que soit l’échelle retenue.
L’exemple de la courbe de Koch, ci-dessous, permet de mieux appréhender le phénomène :
− Le comportement des marchés financiers comme il a été dit ne fait pas exception, les phénomènes irréguliers étant des plus courants.
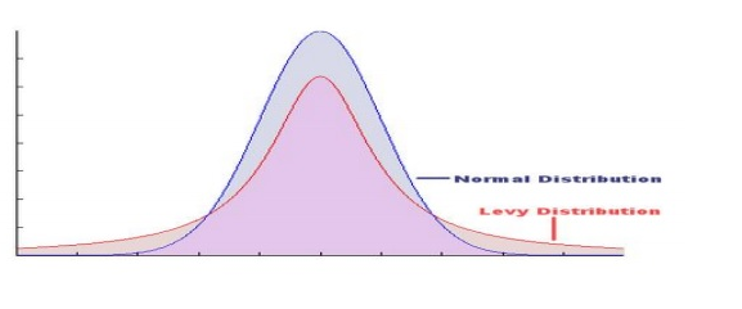
Ainsi, les marchés financiers, d’un point de vue statistique, se caractérisent par une loi de distribution dite « Loi de Lévy Pareto».
Il a été démontré que les écarts de l’indice S&P500 suivent une loi très proche de celle-ci.
Nous n’allons pas ici plus loin dans les détails mathématiques, l’important étant que les queues de distributions de cette loi sont considérablement plus épaisses, c’est-à-dire que les écarts importants par rapport à la moyenne (présence de discontinuité dans l’évolution des cours, chutes brutales des indices, hausses subites d’un ou de plusieurs actifs) sont bien plus fréquents que pour la loi Gaussienne.
Pour caractériser ces comportements, Mandelbrot parlera d’ailleurs d’Effet Noé et d’Effet Joseph.
Le premier cas illustrant une rupture brutale de la tendance en cours, comme lorsqu’un barrage est submergé par une vague d’une hauteur « improbable » (exemple de Fukushima et du tsunami d’une hauteur de 30 m suite au séisme de 2011, bien au dessus des barrières de protection mise en place).
A l’inverse, l’Effet Joseph s’attache à la « mémoire » de marché, c’est-à-dire à la persistance d’une tendance sur différentes périodes de temps. Le marché haussier actuel parti des Etats-Unis depuis fin février 2009 en est un bon exemple.
Comparaison des deux lois de distribution
Un des premiers exemples de fractales utilisées par les opérateurs des marchés financiers concerne l’analyse technique. Si cette approche continue de ne pas faire l’unanimité parmi les professionnels de la finance, certains instruments méritent une attention toute particulière dans le cadre de cet article.
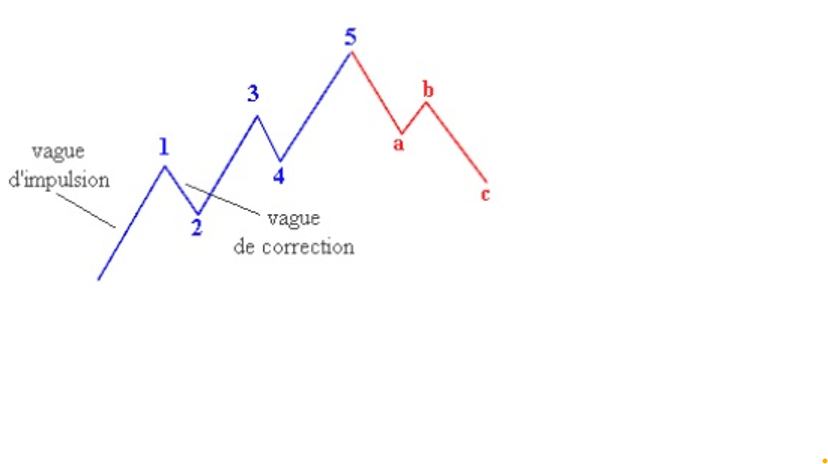
On évoquera les vagues d’Elliott proposé par Ralph Nelson Elliott, dans la première moitié du XXème siècle. Selon cet outil le marché évolue par des séries de vagues successives sous la forme de mouvements irréguliers (vagues d’impulsion en 5 temps (I à V) et vagues de correction en 3 temps (A, B et C )) et ce, quel que soit l’échelle observée (de quelques minutes à plusieurs décennies voire plus) ce qui caractérise bien les fractales. Ajoutons, qu’il existe, notamment, un certain nombre de règles entre les différentes vagues.
Néanmoins, si cette approche a le mérite de mieux visualiser ce que représente le terme fractale pour les marchés financiers, elle est très souvent rejetée par nombres d’intervenants, (certains jugeant même cette approche comme ésotérique !), en raison de la difficulté de sa mise en pratique (par exemple, le point de départ d’un mouvement) qui permet de caractériser la vague en cours et donc son évolution future.
Evolution caractéristique d’un actif selon Elliott
Il existe également d’autres outils, associés aux fractales, qui aident à mieux appréhender les marchés financiers. Ceux-ci permettent d’intégrer un niveau de risque beaucoup plus élevé que dans le cas de modèles de gestion basés sur une Loi de distribution Normale.
C’est par exemple, le cas de l’exposant de Hurst (noté H) 1 qui facilite la caractérisation du comportement d’un actif coté (action, trackers, indices par exemple) à un moment donné.
Dit autrement il permet d’estimer la prévisibilité d’un flux de données de prix. Exprimé de manière plus mathématique, H décrit la structure des variations observées dans les séries financières. Ainsi, si H est inférieur à 0.5, on parlera d’oscillations dominantes ou d’anti-persistance. On observe des séries caractérisée par un retour à la moyenne des cours avec des renversements soudains de tendance. Ainsi une diminution sera suivie d’une augmentation et vice-versa, c’est-à-dire que la tendance ne dure pas. On assiste souvent à une volatilité plus forte qui indique les doutes (les incertitudes) des investisseurs pour un actif donné sur la période retenue.
Dans le cas où H est supérieur à 0.5, on parle de « mémoire » de marché ou de persistance de a tendance dominante, c’est-à-dire que la tendance en cours (positive ou négative) à de très fortes chances de se poursuivre…et on peut donc augmenter la position (à l’achat ou à la vente) sur l’actif concerné. Au fur et à mesure que H se rapproche de 1, la tendance en cours est de plus en plus marquée.
Si H est égale à 0.5, la série subit une alternance aléatoire des tendances et des retours à la moyenne, c’est-à-dire capable d’aller dans n’importe quelle direction…il faut donc mieux s’abstenir d’intervenir dans ce cas sur l’actif retenu. Les marchés où dominent les arbitragistes sont typiques de ce genre de comportement (cas du marché des matières premières, du marché obligataire) mais concerne également le marché des changes sur des paires de devises comme le dollar/yen ou le dollar/euro en raison de l’extrême profondeur de ce type de marchés cotés en continu 24 h sur 24.
Dans le cas d’une Loi Normale ou Gaussienne, l’exposant de Hurst est de 0.5.
La prise de conscience de la nature fractale des marchés remet donc en cause la théorie de l’efficience des marchés encore en application chez nombre d’investisseurs. En effet, l’hypothèse des marchés financiers efficients telle que définie par ’économiste Eugène Fama, prix Nobel d’Economie en 2013, suppose, rappelons-le, que le marché reflète à chaque instant pour un actif donné toute l’information disponible. Il serait alors impossible de battre le marché, sauf à disposer d’informations privilégiées (cas du délit d’initié). Or, dans les cas des cours à structure de persistance (H > 0.5), suivre les tendances peut s’avérer gagnant.
Cette théorie fait également la part belle à la rationalité des investisseurs, concept fortement remis en cause par les recherches en finance comportementale, qui ont montré, en outre, les nombreux biais des intervenants selon le type de marché.
1 D’un point de vue plus mathématique,
Il indique la vitesse à laquelle croît l’amplitude des variations du prix
(« range ») quand on passe à des échelles temporelles de plus en plus grandes. Notons que cette amplitude est
divisée par l’écart-type. C’est le rapport de la « bonne » volatilité des tendances à la « mauvaise » volatilité des piétinements. L’exposant H est directement lié à la complexité de l’évolution. On parle aussi de la dimension
fractale DF = 2 – H. Plus une courbe est haché, plus elle est donc complexe, plus grande est DF et plus petit est H. Notons que H varie entre 0 et 1, et DF entre 1 et 2.
Pour aller plus loin :
« Benoit Mandelbrot et la modélisation mathématique des risques financiers ».
Rama Cont. CNRS – Université Pierre et Marie Curie (Paris VI).
Mandelbrot : Fractales, Hasard et Finance. Editions Champs/ Flammarion.
Sapoval : Universalités et Fractales. Editions Champs/Flammarion.
David Ruelle : Hasard et Chaos. Editions Poches Odile Jacob.
R.Mantegna and H.Stanley: “An introduction to Econophysics”. Cambridge University Press.
